Sorting Algorithms

Sorting is the process of arranging elements in a specific order (ascending or descending). Sorting algorithms like Merge Sort and Quick Sort are essential parts of DSA in Python, especially for optimizing performance. Sorting improves the efficiency of other operations like searching.

Bubble Sort Algorithm

Bubble Sort is a simple sorting algorithm that works by repeatedly comparing adjacent elements in a list and swapping them if they are in the wrong order. This “bubbling” process continues until the entire list is sorted. It is easy to implement and understand, but inefficient for large datasets due to its time complexity of O(n²). It works best for small or nearly sorted lists.

In Python, bubble sort can be implemented using nested loops. The main operations performed in bubble sort are:

• Compare: Check each pair of adjacent elements.
• Swap: Exchange elements if they are in the wrong order.
• Repeat: Continue the process until no swaps are needed.

Bubble sort is widely used for educational purposes, small datasets, and scenarios where simplicity matters more than efficiency.

Example :

Input:

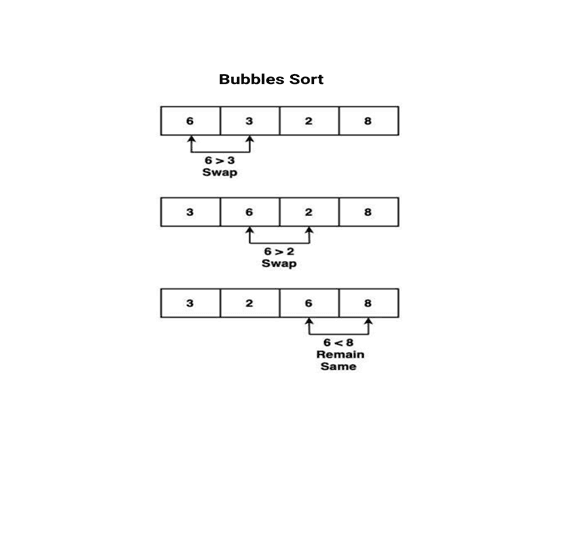
# Bubble Sort
arr = [6,3,2,8]
for i in range(len(arr)):
    for j in range(0, len(arr)-i-1):
        if arr[j] > arr[j+1]:
            arr[j], arr[j+1] = arr[j+1], arr[j]
print("Sorted array:", arr)

Output:

Sorted array: [3,2,6,8]

Merge Sort Algorithm

Merge Sort is a divide-and-conquer sorting algorithm that works by splitting the array into halves, sorting each half recursively, and then merging the sorted halves back together. It guarantees a time complexity of O(n log n) and is a stable sorting algorithm, meaning the relative order of equal elements is preserved.

In Python, merge sort can be implemented using recursion. The main operations performed in merge sort are:

• Divide: Split the array into two halves.
• Conquer/Sort: Recursively sort each half.
• Merge: Combine the two sorted halves into a single sorted array.

Merge sort is widely used in large datasets, external sorting, database systems, and applications where stability is important.

Example:

Input:

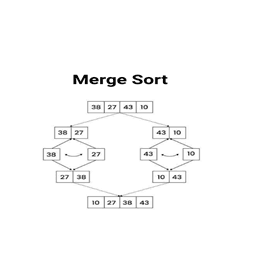
# Merge Sort
def merge_sort(arr):
    if len(arr) > 1:
        mid = len(arr)//2
        L = arr[:mid]
        R = arr[mid:]
        merge_sort(L)
        merge_sort(R)
        i = j = k = 0
        while i < len(L) and j < len(R):
            if L[i] < R[j]:
                arr[k] = L[i]
                i += 1
            else:
                arr[k] = R[j]
                j += 1
            k += 1
        while i < len(L):
            arr[k] = L[i]
            i += 1
            k += 1
        while j < len(R):
            arr[k] = R[j]
            j += 1
            k += 1

arr = [38, 27, 43, 10]
merge_sort(arr)
print("Sorted array:", arr)

Output:

Sorted array: [10,27,38,43]

Quick Sort Algorithm

Quick Sort is a divide-and-conquer sorting algorithm that works by partitioning the array around a pivot element, placing smaller elements on the left and larger elements on the right. It then recursively sorts the left and right partitions. Quick Sort is fast in practice, with an average time complexity of O(n log n), but can degrade to O(n²) if the pivot is poorly chosen.

In Python, quick sort can be implemented using recursion. The main operations performed in quick sort are:

• Choose Pivot: Select an element as the pivot.
• Partition: Rearrange elements so that smaller go left, larger go right.
• Recursive Sort: Apply quick sort on left and right partitions.
• Combine: Merge partitions implicitly as recursion unwinds.

Quick Sort is widely used in large datasets, standard library sorting functions, and applications where average-case efficiency is critical.

Example:

Input:

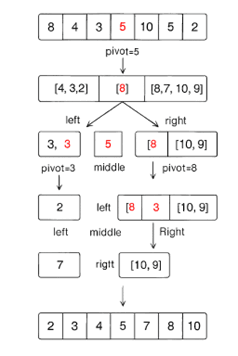
# Quick Sort
def quick_sort(arr):
    if len(arr) <= 1:
        return arr
    pivot = arr[len(arr)//2]
    left = [x for x in arr if x < pivot]
    middle = [x for x in arr if x == pivot]
    right = [x for x in arr if x > pivot]
    return quick_sort(left) + middle + quick_sort(right)

arr = [8,4,3,5,10,5,2]
print("Sorted array:", quick_sort(arr))

Output:

Sorted array: [2,3,4,5,7,8,10]